Roll an
unbiased die twice, note which face turns up each time a die is rolled.
Calculate the probability distribution of a face with number one.
Counting
the total and favorable numbers of outcomes constituting the specified number
of objects sampled with replacement from the finite population is important to
calculate the probability of favorable events. Excel software is commonly
available in the desktop or the laptop and is an important means to calculate
the discrete probability distribution of samples drawn with replacement. I take an example from my Statistical
Note 19, and will show how calculate the multicategory discrete probability distribution
with replacement using Excel function. Refer to that note for conceptual
clarity on using the tree diagram and formula to calculate the Multinomial probability
distribution.
EXCEL
Software
EXCEL
software does not have an inbuilt function to calculate Multinomial
probability. Three inbuilt EXCEL functions are used to calculate the Multinomial
probability. They are - POWER, MULTINOMIAL and PRODUCT functions.
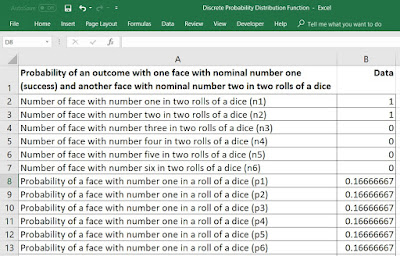
First, I will prepare the dataset for an outcome
constituting one face with nominal number one (A) and another face with nominal
number two (B) in two rolls of a dice. Each face of a dice has an equal chance
of one divided by six (0.1666) as shown in Diagram 1. It is the case of group
two outcomes discussed under Formula section in the Statistical Note 19.
Diagram
1: Dataset showing the number of face in two
rolls of dice and the probability of each face in a roll
Referring to the Multinomial distribution formula, the
POWER function is used for each probability of a face powered by number of
times that face occurs in two rolls of a dice as shown in Diagram 2. The POWER
function has two fields - ‘Number’ and
‘Power’. In Diagram 2, ‘Number’ takes the value as the base number as shown in
Diagram 2. The Power value calculated in the cell B14 has taken the value from the cell ‘B8’.
‘Power’ is the exponent to which the base number is raised. It has taken the
value from the cell ‘B2’. Likewise, the
POWER function is applied to all remaining values from B3 to B13, and placed in
the cells B15 to B19.
Diagram
2: Application of POWER Function in Excel
The MULTINOMIAL
function is applied to calculate the Multinomial coefficient in the Multinomial
distribution formula. The MULTINOMIAL
Function has at least two fields ‘Number1’ and ‘Number2’ as shown in Diagram 3.
These field are used to indicate the number of faces with nominal numbers in
two rolls of a dice in this example. They took the values from B2 to B7 as
indicated in the function argument box and formula bar, and resulted in the
value 2.
Diagram
3: Application of MULTINOMIAL Function in
Excel
The
PRODUCT function is applied to calculate the product of a series of numbers.
The function has several fields – ‘Number1’, ‘Number2’. The first will take a
series of values from cells B14 to B19 on probabilities power by number of
faces with nominal numbers in two rolls of a dice as shown in Diagram 4. The
second field takes the value from the Multinomial coefficient calculated in
cell B20. The PRODUCT function gives the probability of an outcome, an occurrence
of a face with nominal number one and another face with nominal number two in
two rolls of a dice. This value is equal to 0.05555 shown in function argument
box in Diagram 4.
Diagram
4: Application of PRODUCT Function in Excel
This
probability of an outcome, an occurrence of a face with nominal number one and
another face with nominal number two in two rolls of a dice is equal to P(0,1,1,0,0,0)
discussed under Group Two outcomes under Formula section of the Statistical
Note 19.
Similar
process is followed to calculate the probability of each group of outcomes. Finally, adding the probability of each group of outcomes
will give the Multinomial probability distribution.





No comments:
Post a Comment