Converting Multi-category to Two-category Discrete Probability Distribution of Sampling With Replacement, Statistical Note 26

Roll an unbiased die twice, note which face turns up each time a die is rolled. Calculate the probability of an outcome that has a face with one dot in two rolls using two category discrete probability distribution.

Multi-categories of a random variable can be reduced to two categories of an outcome in independent experiments or trails with replacement. This is important because two-category discrete probability distribution with replacement is most commonly as one is concerned with the probability of a successful or failure event. Multinomial distribution is the generalization of Binomial distribution  and thus the Binomial distribution can be used.

Rolling of a dice is a multi-category experiment or a trial. A dice has six faces with one dot (A), two (B), three (C), four (D), five (E) and six (F) dots. Every roll is independent and in every roll any of all mutually exclusive and possible values are likely to occur. The marginal probability of each face in a roll of a dice is one face divided by total of six faces.

I will discuss the process of reducing the multi-categories to two-categories and calculating the two-category discrete probability distribution with replacement using tree diagram, formula and Excel software function. For details on two-category and multi-category discrete probability distributions refer to my statistical notes from 17 to 25.

Tree Diagram

Tree diagram is an important means to visualize, count the number of outcomes and calculate the probability.  There are only two categories, success and failure in each roll of a dice with replacement. Let X be an event that the face A appears in rolling of a dice, also referred to as the success. The marginal probability of X, denoted by P(X) equal to p, is one divided by total of six faces of a dice as discussed above, which is equal to 0.1667. Let Y be an event failure that will consist of five faces with other dots of a dice. Thus, the marginal probability of failure, denote by P(Y) equal to q, is five faces other than the face with one dot is five divided by six, equal to 0.8333. The marginal probabilities P(X) and P(Y) remain the same in the second roll of a dice as in the first roll (Diagram 1).

Diagram 1: Marginal probabilities in two independent rolls of a dice (sampling with replacement)

The joint probability that an event X appears in the first roll and an event Y appears on the second roll, denoted by P(X∩Y), is the product of P(X) and PY) which is equal to five divided by 36, 0.1388. Likewise, the joint probability that an event Y appears in the first roll and an event X appears on the second roll, denoted by P(Y∩X), is the product of P(Y) and P(Y) which is equal to five divided by 36, 0.1388. Thus, the total probability of an outcome that X of two events occurs, is the sum of P(X∩Y) and P(Y∩X), which is equal to 0.2777.

Formula

Formula is another means of calculating the discrete probability distribution. Let X be a random variable of interest that takes one of 0, 1 or 2 values as the number of face with one dot in two rolls of a dice, denoted by ‘x’. The probability distribution of X depends on the parameters, ‘n’ and ‘p’, and is given by the expression

P(X=x) = C(n,x)p^xq^n-x

This distribution is referred to as Binomial distribution.

In this example, n=2 and p=1/6, q=5/6 and ‘x’ takes the value one. Putting these values in the above formula, one gets

P(X=1) = [C(2,1) X (1/6)¹ X (5/6)¹] = (2 X 5)/ (6 X 6) = 0.2777

EXCEL Function

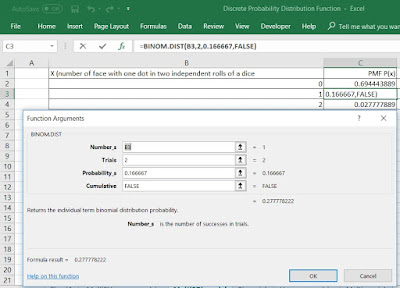
Excel software is commonly available in the desktop or the laptop and is an important means to calculate the discrete probability distribution. Excel software has the ‘BINOM.DIST’ function having four fields. ‘Number_s’ takes the number of successes in trials. In this example, a face with one dot in two independent rolls of a dice has been used as shown in the cell B3 of the table as well as the function argument box in Diagram 2.

Diagram 2: ‘BINOM.DIST’ Function Arguments Using Dataset in Excel Worksheet and using ‘FALSE’ logical value in the field ‘Cumulative’

The field ‘Trials’ is the number of independent trials. In this example, two independent rolls of a dice were considered shown in the function argument box of Diagram 1.

The field ‘Probability’ is the probability of success on in any individual trial. A probability value lies between 0 and 1. In this example, the probability of a face with one dot is one of six faces, equal to 0.16667, as shown in the field of the function argument box of Diagram 1.

The field ‘Cumulative’ is a logical value that determines the form of the function. If ‘Cumulative’ is ‘FALSE’, ‘BINOM.DIST’ calculates the probability mass function (PMF), which gives the probability associated with the value assigned to the field ‘Number_s’ as the number of successes. It is shown in the function argument box in Diagram 1.

Fixing all four fields in the function arguments, ‘BINOM.DIST’ function calculated the PMF equal to 0.2777. It means that there is 27.7 percent chance that a face with one dot will appear in two independent rolls of a dice. 

The probability calculated using Excel software function is equal to the values calculated in tree diagram and formula sections above. Discussion in this note indicates that the multi-category can be reduced to two-category in which one category will be considered as a successful event and another as a failure event. Then, Binomial distribution can be applied to two category discrete probability distribution. This will limit the use of multinomial probability distribution. This is important also because two-category discrete probability distribution is most commonly as one is concerned with the probability of a successful or failure event.  Another learning is that both manual and auto calculation produce the same values and are useful to calculate the discrete probability distribution with replacement. Conceptual understanding is a backbone and automatization is efficient. Thus, both are important knowledge and skill sets.